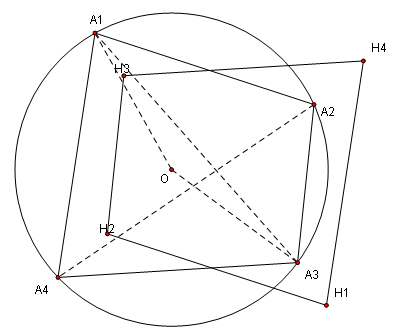
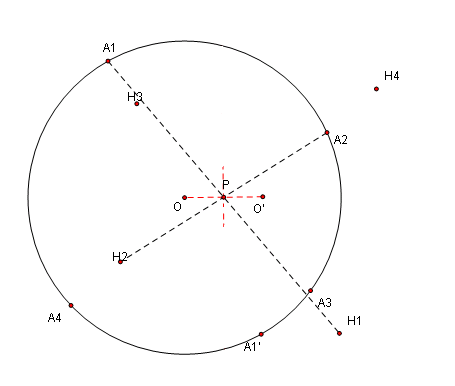
设 A1A2A3A4 为圆 O 的内接四边形，H1、H2、H3、H4 依次为 …
… △A2A3A4、△A3A4A1、△A4A1A2和△A1A2A3 的垂心。
求证：H1、H2、H3、H4 四点共圆。并定出该圆圆心。
….
..
.
.
.
.
.
（
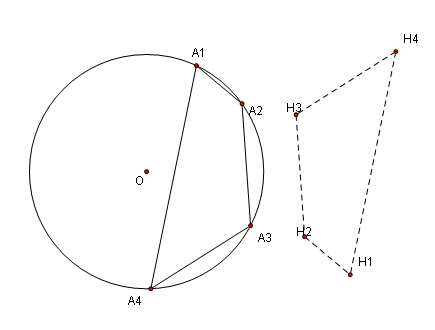
观察，为了不受干扰起见，先擦去各种垂线，调整位置，使得生成的四边形在圆外的某个位置。
… 看起来四个垂心之所以共圆的缘故应该是同先前的圆内接四边形关于某个点中心对称所致。
… 那么图里面应该有不少平行四边形 …
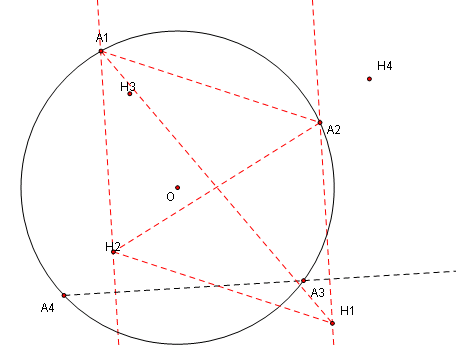
连接 A1H1，A2H2，易知 A1H2 // A2H1，那么欲证四边形 A1A2H2H1 是平行四边形，还需要得到A1A2 // H2H1。
但是不容易直接证另一组线段平行（证对角线互相平分看起来也没有什么希望的样子）……
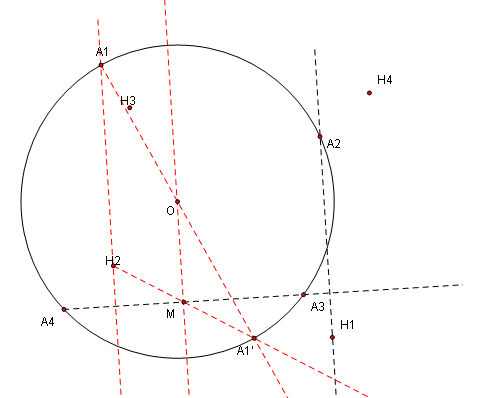
引入辅助线，可以通过 OM 将 A1H2，A2H1进一步联系起来… 反复用这个手法，之后我们可以得到四组平行四边形（每条底边证一个），一共可以得到八组对角线形成的中心对称关系。而只有四组对应点，因而每一组对应点得到了两个对应关系，实际的结果则是得到了这四个平行四边形拥有一个共同的对角线交点，也就是要找的对称中心，记作点 P，接下来作出圆心 O 的中心对称点 O’ 即可。
）
因为 A1H2，A2H1 分别都在线段 A3A4 的一条垂线上，所以 A1H2 // A2H1。
作 A3A4 的垂径 OM，根据平行线等分线段定理，M 同时也是 H2A1 的中点，
再根据三角形中位线定理，知 A1H2 = 2OM。
同理，A2H1 也等于 2OM。
因而四边形 A1A2H1H2 是平行四边形。连接对角线交点 P，已不难得知 H1、2、3、4 和 A1、2、3、4，关于点 P 中心对称。因而 H1、H2、H3、H4 四点共圆。
连接 OP，并延长 OP 到 O’，使得 PO = PO’，则 O’ 是所要求的圆心。
Q.E.D.
