Brief description:
…
Analysis:
…
算法一：cdq 分治
随着科技的进步我们已经知道可以使用 cdq 分治来解决这类问题了。。。
//}/* .................................................................................................................................. */
const int N = int(1e5) + 9;
DB A[N], B[N], R[N], f[N];
int n;
#define y(i) (f[i] / (R[i] * A[i] + B[i]))
#define x(i) (R[i] * y(i))
bool cmp_k(int i, int j){
return A[i]*B[j] < A[j]*B[i];
}
void cdq(int l, int r){
if (l + 1 == r){
checkMax(f[r], f[l]);
}
else{
int m = l + r >> 1; cdq(l, m);
static Po P[N], C[N]; int pn = 0, cn = 0;
FOR(i, l, m) P[pn++] = Po(x(i), y(i)); sort(P, P+pn);
REP(i, pn){
while (cn > 1 && dett(C[cn-1], C[cn], P[i]) >= 0) --cn;
C[++cn] = P[i];
}
static int Q[N]; int qn = 0;
FOR(i, m, r) Q[qn++] = i; sort(Q, Q+qn, cmp_k);
#define eval(c) (A[i]*C[c].x + B[i]*C[c].y)
int c = 1; REP(q, qn){
int i = Q[q]; while (c < cn && eval(c) < eval(c+1)) ++c;
checkMax(f[i], eval(c));
}
cdq(m, r);
}
}
int main(){
#ifndef ONLINE_JUDGE
//freopen("in.txt", "r", stdin);
freopen("cash7.in", "r", stdin);
//freopen("out.txt", "w", stdout);
#endif
RD(n); RF(f[0]); REP(i, n) RF(A[i], B[i], R[i]);
cdq(0, n); OT(f[n]);
}
https://gist.github.com/lychees/6f7e2fb392c24da5bd16#file-cdq_o-nlog2n-cpp
//}/* .................................................................................................................................. */
const int N = int(1e5) + 9;
DB A[N], B[N], R[N], f[N];
int n;
#define y(i) (f[i] / (R[i] * A[i] + B[i]))
#define x(i) (R[i] * y(i))
bool cmp_k(int i, int j){
return A[i]*B[j] < A[j]*B[i];
}
int Q[N]; Po C[N], P[N];
void cdq(int l, int r){
if (l + 1 == r){
checkMax(f[r], f[l]);
P[l] = Po(x(l), y(l));
}
else{
int m = l + r >> 1;
static int tmp[N]; int tl = l, tr = m;
FOR(i, l, r) if (Q[i] < m) tmp[tl++] = Q[i]; else tmp[tr++] = Q[i];
memcpy(Q+l, tmp+l, sizeof(int) * (r-l));
VP Pl, Pr; cdq(l, m);
int cn = 0; FOR(i, l, m){
while (cn > 1 && dett(C[cn-1], C[cn], P[i]) >= 0) --cn;
C[++cn] = P[i];
}
#define eval(c) (A[i]*C[c].x + B[i]*C[c].y)
int c = 1; FOR(q, m, r){
int i = Q[q]; while (c < cn && eval(c) < eval(c+1)) ++c;
checkMax(f[i], eval(c));
}
cdq(m, r);
static Po tmpP[N]; merge(P+l, P+m, P+m, P+r, tmpP);
memcpy(P+l, tmpP, sizeof(Po)*(r-l));
}
}
int main(){
#ifndef ONLINE_JUDGE
//freopen("in.txt", "r", stdin);
freopen("cash7.in", "r", stdin);
//freopen("out.txt", "w", stdout);
#endif
RD(n); RF(f[0]); REP(i, n) RF(A[i], B[i], R[i]), Q[i] = i; sort(Q, Q+n, cmp_k);
cdq(0, n); OT(f[n]);
}
https://gist.github.com/lychees/6f7e2fb392c24da5bd16#file-cdq_o-nlogn-cpp
算法二：平衡树维护凸壳
。。。看来还是贾教（Oimaster）解释的最清楚。。0 w0。
根据提示内容，我们就可以得到一个动态规划算法：用f[i]表示到第i天为止能得到的最多钱数。根据f[i]，我们可以得到如果第i天卖出金券的话，A券和B券各有多少张（我们设为X[i]和Y[i]）。则转移方程为：
f[i] = max( f[i-1], max{ X[j]*a[i] + Y[j]*b[i] | j <= i}) 边界条件为f[1]=s。 其中X[i]和Y[i]可以根据f[i]得出，具体就不讲了。
const int N = 109;
DB A[N], B[N], R[N], f[N];
int n; DB ans;
int main(){
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
//freopen("out.txt", "w", stdout);
#endif
RD(n); RF(f[0]); REP_1(i, n) RF(A[i], B[i], R[i]);
#define b(i) (f[i] / (R[i] * A[i] + B[i]))
#define a(i) (R[i] * b(i))
REP_1(i, n){
f[i] = f[i-1];
REP(j, i) checkMax(f[i], a(j)*A[i] + b(j)*B[i]);
}
OT(f[n]);
}
这个动态规划显然是1D/1D动态规划，普通做法的时间复杂度为O(n^2)，对于100000的数据显然是会超时的，所以还要优化。
我们把所有的X[i]和Y[i]抽象成坐标系中的点，即X[i]为横坐标，Y[i]为纵坐标。
然后我们令P=a[i]*x+b[i]*y，即转移方程中的(X[j]*a[i]+Y[j]*b[i])。变形可得y=(-a[i]/b[i])*x+P/b[i]，即有一条斜率一定的直线，并且经过某个点(x,y)，然后要最大化截距。对于这个问题，我们可以想象成有一条斜率为(-a[i]/b[i])的直线从无穷远的地方向下，第一个碰到的点即为最优解。那么就可以得到以下结论：
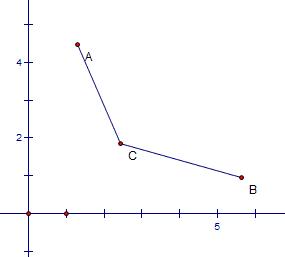
如果点(X[i],Y[i])为某次的最优决策，那么显然这个点是在所有点的凸壳上的，如下图中的C点不可能为最优的决策点。
原因很简单，如果有一条斜率一定直线从上向下平移过来，必定先碰到点A或点B，不可能先碰到点C。
因此我们维护一个决策序列，这个决策序列中的点即为凸壳上的点，然后我们按横坐标将这些点排序，则纵坐标也就有序，并且相邻两个点的连线的斜率单调递减。
对于一条斜率一定的直线，其最优解的点必然是这样的：
即如果这条直线的斜率为k，最优决策点与其相邻两点连线的斜率分别为k1和k2，则满足k1>=k>=k2。
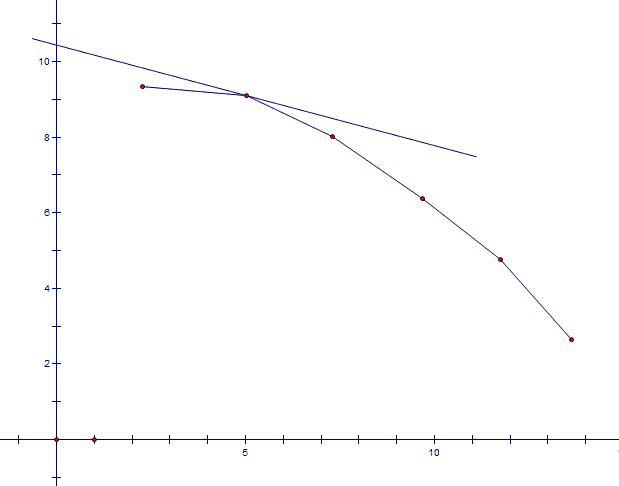
因此现在我们的任务是怎样高效地维护这个决策点序列，显然平衡树可以很好的做到这点。我们将这些点按照横坐标的大小建一棵平衡树，那么纵坐标也有序，然后每新算出来一个f[i]，算出与其对应的X[i]与Y[i]，先按横坐标找到这个点的插入位置。然后我们判断这个点是否应该保留，如果出现第一幅图中的情况，那么这个点无需插入，否则将这个点插入平衡树中。下面就是维护这个凸壳，我们从这个点开始，分别向左和向右找到第一个满足凸壳的两个点，将中间的点删除。对于取得f[i]最优决策，因为斜率单调减，因此我们可以二分（即判断这个点是在左子树中还是右子树中）。其中凸壳维护过程如下图所示
struct node{
static node*NIL,*root; // 哨兵、根结点 .. .
node*c[2],*p; PDD o; DB k[2]; // 孩子、父亲、坐标、斜率。。
}
.. .
inline void clean(int d){
for (node*x=neighbor(d);x!=NIL;x=neighbor(d)){ //x->o.se < o.se ^ d
if (x->splay(this)->k[d] < get_k(o, x->o) ^ d) setc(d, x->c[d]);
else break;
}
}
inline void clean(){
clean(0), clean(1);
}
inline node*fix(){
splay(); node*a = pred(),*b = succ();
k[0] = a == NIL ? +OO : get_k(o, a->o);
k[1] = b == NIL ? -OO : get_k(o, b->o);
if (k[0] < k[1]){
root = a->splay(this), a->p = NIL, a->setr(r);
}
else {
clean(), a = pred(), b = succ();
k[0] = a == NIL ? +OO : a->k[1] = get_k(o, a->o);
k[1] = b == NIL ? -OO : b->k[0] = get_k(o, b->o);
}
}
.. .
// x->k[0] > k > x->k[1]
node*Find(DB k){
for (node*x=root;;){
if (x->k[0]<k) x=lx; else if (k<x->k[1]) x=rx;
else return x;
}
}
void Insert(node*z){
node*x=root,*y=NIL; for(;x!=NIL;y=x,x = x->c[z->o>x->o]);
if (y == NIL) root = z; else y->setc(z->o>y->o, z);
z->fix();
}
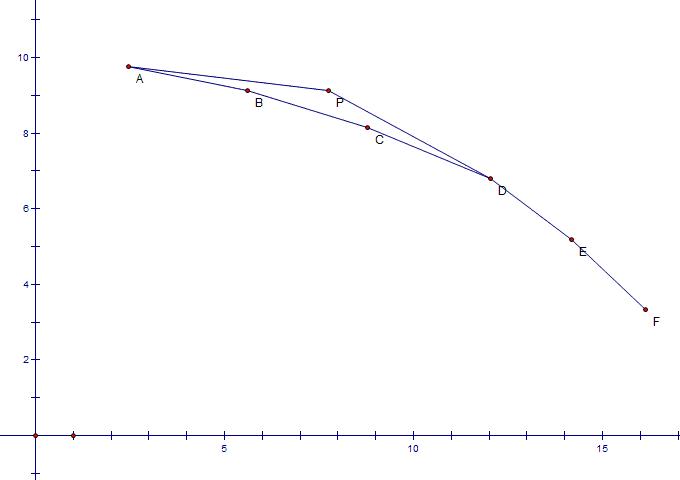
（我们现在插入点P，则点B和点C将被删除）
最后讨论平衡树的选择，这题实际上用哪种平衡树都是可以的，但最方便的无疑是Splay，如果我们选择插入点P，那么我们将点P旋转到根节点，然后找到P的前驱（即左子树中最大的），判断是否删除，如果删除，那么继续上述过程，然后再对右子树进行维护。最终复杂度O(nlogn)，完全可以对付100000的数据。
最后想说的是，这题编程中的细节比较多，如遇到横坐标相同的点怎么办，甚至横纵坐标都相同的点怎么办，所以编程之前要想清楚一些细节问题。
Splay 维护凸壳。。（斜率。。600ms +-
Splay 维护凸壳。。（叉积。。550ms–
External link:
http://www.lydsy.com/JudgeOnline/problem.php?id=1492
http://hi.baidu.com/oimaster/item/d8041f4a865444ee1f19bc43
种田君。。
