传送门
https://codeforces.com/contest/1552
Table of Contents
Problem C.
给定一个圆环，初始已经连了一些线段，要求连剩下的线段，问最优情况下，最后总交点最多是多少。
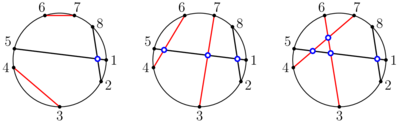
不考虑已经连的线段，对于剩下的我们按照最优情况 1234..1234.. 这样连就行。。
最后把已经连的拉进来一起统计即可。
btw，圆周上均匀分布的 n 个点互相连线可将圆分为多少块？
Problem D.
给定一个长度为 n 的序列 a，问是否可以构造一个长度同样为 n 的序列 b，使得 a 中的每个元素都是 b 中某两个元素的差。
n <= 10
Problem E. Colors and Intervals
给 n 种颜色，初始时给长度为 n*k 个位置染色，使得每种颜色恰好出现 k 次。
求构造 n 组区间的方案，满足对于每种颜色，都有一组区间的端点是这种颜色。
且，不存在某个位置，使得被区间覆盖超过 \ceil{n, k-1} 次。
(n, k <= 100)
贪心？显然我们总是选择那些尽可能小的区间，因此对于每种颜色，我们只需要考虑 k-1 种相邻的区间即可。
我们按照所有区间大小排序来依次选择？很遗憾这样是错的。但是稍微改改，按照每个区间的右端点来排序就对了。
证明？反证法。
考虑某种颜色，我们枚举了所有 k-1 种区间发现都不满足，那么对于这些区间 [a, b]，
每个区间都存在 \ceil{n, k-1} 个区间使得它们的右端点均位于 [a, b] 的内部，因为覆盖 [a, b] 的区间因为右端点比 b 大还没有被我们扫描到。
那么此时一共已经选择了 (k-1)*\ceil{n, k-1} >= n 个区间，但是我们还没有选择那么多，与假设矛盾。
Problem H. Guess the Perimeter
格点图里 ( <= 200) 有一个矩形，你可以至多 4 次询问后回答这个矩形的周长。
每次询问，你可以挑选任意数目的点，返回里这个集合中有多少点在目标举行的内部或者边缘。
???
Problem F. Telepanting
数轴上有 n 个传送门，每个传送门用三元组表示为 (xi, yi, {0,1})，表示传送门所在位置为 xi，传送的目标位置为 yi，以及当前是否 active。（yi < xi）
有一只蚂蚁从 0 出发，每个单位时间向右移动一格，当走到传送门时，如果 inactive 则变为 active，如果 active 则被传送至 yi 并置该传送门为 inactive。
问走到 xn + 1 需要多少时间。
走到某个传送门时，不管这个传送门当前的状态是 inactive 还是 active，前面的传送门一定当前都是 active。
因为所有的传送门都是往后退，那么要突破某个传送门，一定走上去的时候是 inactive，通过之后翻成 active。
这样状态就很简单了，a[i] 表示第 i 个传送门的状态是 active，那么走上去之后传送走到下次回来需要花费多少时间。
转移方程是 …
a[i] += x[i]-y[i];
REP(j, i) if (x[j] >= y[i]) a[i] += a[j];
用前缀和 + 二分查找优化即可。
Problem I. Organizing a Music Festival
求有多少长度为 n 的排列，满足某些集合出现在连续位置。
(n <= 100)
有点意思。
首先不妨弱化，只考虑集合 size = 2 的情况。
那么显然每个集合相当于一条边，于是我们转化为一个图论计数问题。
对于每个连通块，要么 * 1 如果 size = 1。
要么 * 2 如果 size >= 2 并且是一条链（正反两种情况）。
要么 * 0 如果 size >= 2 且不是链。
最后再乘以 连通块数 的阶乘即可。
对于一般情况？构成了某种奇妙的树形结构，上面的点和边都变成节点的集合，dfs 进去边 reduce 边统计即可。
（我傻了，这不是 PQ 树么。。。）
