Brief description:
Problem A. About Bacteria
… 培养皿中的 x 只细菌下一秒会繁衍出 kx+b 只细菌。。(。。。
问如果初始培养皿中有 t 只细菌,至少多少秒才可以繁衍出不少于 z 只细菌。
。。。z 为初始为一只细菌时,繁衍 n 秒的细菌总数。。。(。。。
(略,算术题。。不要把 z 真给算出来即可。。
Problem B. Jumping on Walls
一个忍者在一个坑里, 左右各有一面墙,墙上有一些障碍,初始在最下角。
每秒钟可以上下移动一格,或者跳到对面墙的恰好 +k 位置。。
。。问最终能出跳出这个坑。。
(略, Hash Dp 或者 BFS() 都行。。。。
Problem C. Delivering Carcinogen
给定一颗行星坐标 (xp, yp),轨道半径 R,围绕恒心运转的线速度 vp,
以及一个飞船坐标 (x, y),飞船速度 v。。问到达 p 星球的最少时间。。
。。飞船运行过程中距恒星的距离不得低于 r。。(r ≤ R) …
Problem D. Cube Snake
给定一个 n 阶立方体,要求构造满足下列性质的路径:
对任意的 k < n, 存在至少 2 个 k 阶子立方体, 满足其中的数字取自一段连续区间。
Problem E. Gripping Story
空间中有一堆吸盘。
。。每个吸盘用 (xi, yi, mi, pi, ri) 表示。。。
。。自身坐标,重量。。。能抓起来的最大物品的重量,以及作用范围。。。。
。。现给定飞船初始坐标。。(x0, y0)。。初始吸盘(p0, r0)...
问最多可以收集多少个吸盘。。。
(。。一旦得到一个吸盘以后以后就可以无限更换使用。。
(。。。注意注意飞船本身不动不动不动!。。并且吸盘吸到飞船里才能使用。。。OOrz。。
Analysis:
Problem C. Delivering Carcinogen
先避免讨论旋转过程。。。二分答案 x 。。然后行星 p 直接瞬移到它该出现的位置。。。然后判断 d(p’) <= x*v ..
然后子问题 d(p') 就是构造飞船绕道这个位置的最短路径。。根据两条切线产生的夹角分情况讨论。。(
大概有2种情况。。一种是直线。。第二种是 2 条切线 + 1段圆弧。。。
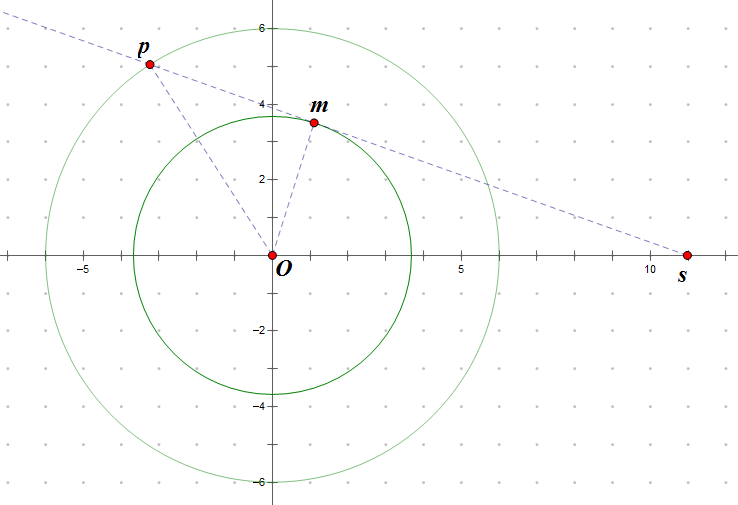
。。。先旋转 s 点到 x 轴上。。。考虑边界情况、把 p 点移动到距离 s 点最远的仍可直线访问的位置。。(称为临界情况。
那么这里的 ∠sOp 是一个重要的常数。。(p 点在更靠左位置的话就是 2条切线 + 1段圆弧的情况了。。
可以解 △pOm 和 △sOm 这两组直角三角形得到。。。(m 是切点。。
。。(同时注意到 2条切线 + 1段圆弧情况时 2条切线 的长度固定不变,就是图中的 pm + ms 。
(代码中的 alpha 是初始旋转角,beta 是临界情况时的 ∠sOp 。。
。。 theta 是当前 p 点具体所在位置。。。delta 是扇形的弧度。。)
const int N = 100009;
Po s, p, o;
DB R_, R, r, ss, vs, vp;
DB alpha, beta, theta, delta;
inline void _R(DB &x){
x = fmod(x, 2*PI); if (x < 0) x += 2*PI;
}
DB d(){
if(theta <= beta || theta >= 2*PI - beta) return sqrt(sqr(R_) + sqr(R) - 2*R_*R*cos(theta));
else{
delta = PI - beta - fabs(PI - theta);
return ss + delta * r;
}
}
bool f(DB x){
//cout << x << endl;
theta = x * vp + alpha, _R(theta);
return d() <= vs * x;
}
int main(){
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
p.input(), RD(vp), s.input(), RD(vs, r);
R_ = s.length(), R = p.length(), vp /= R;
ss = sqrt(sqr(R_) - sqr(r)) + sqrt(sqr(R) - sqr(r));
alpha = p.atan() - s.atan(), _R(alpha);
beta = acos(r / R_) + acos(r / R), _R(beta);
DB ll = 0, rr = (ss + PI*R) * vs;
REP(i, 100){
DB m = (ll + rr) / 2;
if (f(m)) rr = m; else ll = m;
}
OT(ll);
}
Problem D. Cube Snake
给定一个 n 阶立方体,要求构造满足下列性质的路径:
对任意的 k < n, 存在至少 2 个 k 阶子立方体, 满足其中的数字取自一段连续区间。
个人认为是这套题里面思维复杂度最高的一道。。嘛。。(虽然题目一读就明白。。。
首先对解做一定的猜测:
。。最终解是美的。。(。。大概至少也要是递归的、对称的这样。。)。。
。。可能要奇偶讨论。(。甚至更复杂的讨论。。总之比较理想的构造方案可以尽量避免讨论。或者讨论前后共同的部分比较多。)。。
大概就是这类题的一个方向。。需要讨论的地方越多。。甚至最终解不是对称的话这类题的难度就会大大增加。。。
比较科学的方法还是归纳二维情况。。
定义红线和蓝线。分别为两个活动端点。(一个递增一个递减。。
假设现在前面小于等于 k 阶情况已经全部满足,现在得到一个 k*(k+1) 的矩形,并且活动端点处在对角位置。
那么互相向相反方向绘一段线即可得到 (k+1) 阶的情况。。。、
最后到 n 以后随便砍掉一次就能得到结果。。。
二维的代码好像不太难实现。。0w0。
[cpp collapse="true" firstline="1" highlight="" title="我是⑨我只能理解低维世界.cpp"]
const int N = 109;
int A[N][N], ox, oy;
int n, p, q;
const int Red = 0, Blue = 1;
const int Right = 0, Down = 1, Left = 2, Up = 3;
void spin(int n, int c, int d){
if (c == Red){
switch (d){
case Right:
REP(i, n) A[ox][oy + i] = q--;
break;
case Down:
REP(i, n) A[ox + i][oy + n] = q--;
break;
case Left:
DWN(i, n, 0) A[ox + n][oy + i] = q--;
break;
default:
DWN(i, n, 0) A[ox + i][oy] = q--;
}
}
else {
switch (d){
case Right:
REP(i, n) A[ox + 0][oy + i] = p++;
break;
case Down:
REP(i, n) A[ox + i][oy + n] = p++;
break;
case Left:
DWN(i, n, 0) A[ox + n][oy + i] = p++;
break;
default:
DWN(i, n, 0) A[ox + i][oy] = p++;
}
}
}
void gao(){
ox = n, oy = n, q = 0;
A[ox + 0][oy + 0] = 1, A[ox + 0][oy + 1] = 4;
A[ox + 1][oy + 0] = 2, A[ox + 1][oy + 1] = 3; if (n == 2) return;
A[ox + 0][oy + 2] = 5; A[ox + 1][oy + 2] = 6, p = 7;
FOR_1(cur, 3, n){
if (cur&1) --ox; else --oy;
spin(cur, Red, (Down + cur) % 4);
spin(cur, Blue, (Up + cur) % 4);
}
}
void print(){
if (n % 4 == 0) ++oy; else if (n % 4 == 1) ++ox;
REP(x, n){
REP(y, n) printf("%d ", A[ox + x][oy + y] - q);
puts("");
}
}
int main(){
#ifndef ONLINE_JUDGE
//freopen("in.txt", "r", stdin);
#endif
while (scanf("%d", &n) != EOF && n){
if (n == 1) puts("1");
else gao(), print();
}
}
[/cpp]
。。。那么从二维到三维情况稍稍复杂了一点。。。
比较值得考虑的问题是如何让前后两阶的活动端点都处在相同的位置。。或者至少也处在同一个面彼此互换个位置。。。)
(。。三维的情况如果写脑残的话比较难以 Debug。。我后来写一个函数来观察某个角度的视图。。)
[cpp collapse="true" firstline="1" highlight="" title="Problem D. Cube Snake.cpp"]
const int N = 109;
int A[N][N][N], ox, oy, oz;
int n, p, q;
void watchFront(){
n += 2; REP(i, n){
REP(j, n) printf("%d ", A[ox + i][oy][oz + j] - q);
puts("");
}
}
void gao(){
ox = n, oy = n, q = 0;
A[ox + 0][oy + 0][oz + 0] = 1, A[ox + 0][oy + 0][oz + 1] = 4;
A[ox + 0][oy + 1][oz + 0] = 2, A[ox + 0][oy + 1][oz + 1] = 3;
A[ox + 1][oy + 0][oz + 0] = 6, A[ox + 1][oy + 0][oz + 1] = 5;
A[ox + 1][oy + 1][oz + 0] = 7, A[ox + 1][oy + 1][oz + 1] = 8;
if (n == 2) return;
A[ox + 2][oy + 0][oz + 0] = 11, A[ox + 2][oy + 0][oz + 1] = 12;
A[ox + 2][oy + 1][oz + 0] = 10, A[ox + 2][oy + 1][oz + 1] = 9;
p = 13;
int x, y, z; bool rev = false;
#define Blue (rev ? q-- : p++)
#define Red (rev ? p++ : q--)
FOR_1(cur, 3, n){
if (cur & 1){
--oy; REP(i, cur-1) A[ox][oy][oz + i] = Red;
DWN(i, cur-1, 0){
if (i&1) DWN_1(j, cur-1, 1) A[ox + j][oy][oz + i] = Blue;
else REP_1(j, cur-1) A[ox + j][oy][oz + i] = Blue;
}
x = 0, y = 0, z = cur - 1;
A[ox + x][oy + y][oz + z] = Red;
REP_1(i, cur - 1){
if (i&1){
++x; --y; REP(j, i+1) A[ox + x][oy + ++y][oz + z] = Red;
REP(j, i) A[ox + --x][oy + y][oz + z] = Red;
}
else {
++y; --x; REP(j, i+1) A[ox + ++x][oy + y][oz + z] = Red;
REP(j, i) A[ox + x][oy + --y][oz + z] = Red;
}
}
--oz;
x = cur - 1, y = 0, z = 0;
A[ox + x][oy + y][oz + z] = Blue;
REP_1(i, cur - 1){
if (i&1){
--x; --y; REP(j, i+1) A[ox + x][oy + ++y][oz + z] = Blue;
REP(j, i) A[ox + ++x][oy + y][oz + z] = Blue;
}
else {
++y; ++x; REP(j, i+1) A[ox + --x][oy + y][oz + z] = Blue;
REP(j, i) A[ox + x][oy + --y][oz + z] = Blue;
}
}
}
else{
--oy; REP(i, cur) A[ox][oy][oz + i] = Red;
DWN(i, cur, 0){
if (i&1) DWN_1(j, cur-2, 1) A[ox + j][oy][oz + i] = Blue;
else REP_1(j, cur-2) A[ox + j][oy][oz + i] = Blue;
}
x = cur - 1, y = 0, z = 0;
A[ox + x][oy + y][oz + z] = Blue;
REP_1(i, cur - 1){
if (i&1){
--z; ++y; REP(j, i+1) A[ox + x][oy + y][oz + ++z] = Blue;
REP(j, i) A[ox + x][oy + --y][oz + z] = Blue;
}
else {
++z; --y; REP(j, i+1) A[ox + x][oy + ++y][oz + z] = Blue;
REP(j, i) A[ox + x][oy + y][oz + --z] = Blue;
}
}
--ox, x = 0, y = 0, z = cur - 1;
A[ox + x][oy + y][oz + z] = Red;
REP_1(i, cur - 1){
if (i&1){
++y; ++z; REP(j, i+1) A[ox + x][oy + y][oz + --z] = Red;
REP(j, i) A[ox + x][oy + --y][oz + z] = Red;
}
else {
--z; --y; REP(j, i+1) A[ox + x][oy + ++y][oz + z] = Red;
REP(j, i) A[ox + x][oy + y][oz + ++z] = Red;
}
}
rev = !rev;
}
rev = !rev;
}
}
void print(){
if (n % 4 == 3) ++oz; else if (n % 4 == 0) ++ox;
REP(x, n){
REP(y, n){
REP(z, n) printf("%d ", A[ox + x][oy + y][oz + z] - q);
puts("");
}
puts("");
}
}
int main(){
#ifndef ONLINE_JUDGE
//freopen("in.txt", "r", stdin);
#endif
while (scanf("%d", &n) != EOF && n){
if (n == 1) puts("1");
else gao(), print();
}
}
[/cpp]
Problem E. Gripping Story
。。。坐标信息在这题里没有几何意义的。。于是抽象以后就成了维护一堆数列的问题。。。
。。可以树状数组套平衡树裸搞。。。。




 Alca
Alca Amber
Amber Belleve Invis
Belleve Invis Chensiting123
Chensiting123 Edward_mj
Edward_mj Fotile96
Fotile96 Hlworld
Hlworld Kuangbin
Kuangbin Liyaos
Liyaos Lwins
Lwins LYPenny
LYPenny Mato 完整版
Mato 完整版 Mikeni2006
Mikeni2006 Mzry
Mzry Nagatsuki
Nagatsuki Neko13
Neko13 Oneplus
Oneplus Rukata
Rukata Seter
Seter Sevenkplus
Sevenkplus Sevenzero
Sevenzero Shirleycrow
Shirleycrow Vfleaking
Vfleaking wangzhpp
wangzhpp Watashi
Watashi WJMZBMR
WJMZBMR Wywcgs
Wywcgs XadillaX
XadillaX Yangzhe
Yangzhe 三途川玉子
三途川玉子 About.me
About.me Vijos
Vijos
