传送门
Table of Contents
因为疫情原因，今年去年的 Final Adpot 了「宁理规则」，变成了 15 个题三人三机。。。
预感趣味性和策略性可能会降低好多，虽然 CF 上有红名大佬出来倡议反对这个规则，不过好像并不会改变什么。。。（BTW，结果这个题主本届 World Final 直接 win 了，可见他是真的关心这个比赛。。。）
事实也确实如此，感觉题目难度也比前几天的莫斯科邀请赛降低了好多。。变成手速 round 了。。。
(据说这场 8 个题才算签到。。可怕。。。)
以下按照我认为的难度排序。。。
Problem C. Domes
半平面交模板题。
Problem E. Landscape Generator
区间加减等差数列，单点询问。
显然可以线段树，不过这种只在最后询问一次的话用差分+部分和技巧就可以，签到题！
Problem G. Opportunity Cost
假设没有 max 0 这个操作，那么可以 O(n) 扫过去。
进一步观察，我们枚举 shadow 掉哪些维即可，最大值不变。
Problem O. Which Planet is This?!
分别处理每个纬度，差分之后转换成字符串问题，KMP 出所有匹配位置得到所有合法位移。
判断每个纬度的合法位移交集是否为空即可，这种看起来时几何的题最后发现可以用字符串算法通过的题目还是很有趣的，参见 HDU 3918。。
Problem D. Gene Folding
我们可以 dp 出 i 位置向左和向右最大可以折叠掉多少位置。
（就像是我们在最优子矩形里，用单调栈处理出以 i 位置为最小值，向左和向右最远可以延伸到哪里一样）
这个需要我们先预处理出每个位置的回文半径，Manacher 或者 字符串 hash 均可。
Problem I. Quests
问题等价于求出最多有多少 xp 可以获得 bonus。
由于值域不大，考虑暴力 01 背包。
我们只需要对每个物品，预处理出如果要取到它的话，最大可能的背包容量是多少。
我们根据这个值从小到大依次处理每个物品即可。
Problem F. Ley Lines
平面上有 n 个点，用一条宽度为 r 的直线，最多可以覆盖多少点。
可以 O(n2) 枚举直线，然后再对每个点求出合法偏移量的区间，对每个区间分成 +1 -1 两个事件，排序后扫一遍即可，不过复杂度 O(n3)，
进一步考虑，一定存在一组解，使得某个点在笔刷的边界上，因此我们 O(n) 枚举中心，然后用类似 Master Spark 里极角排序的方法处理即可。
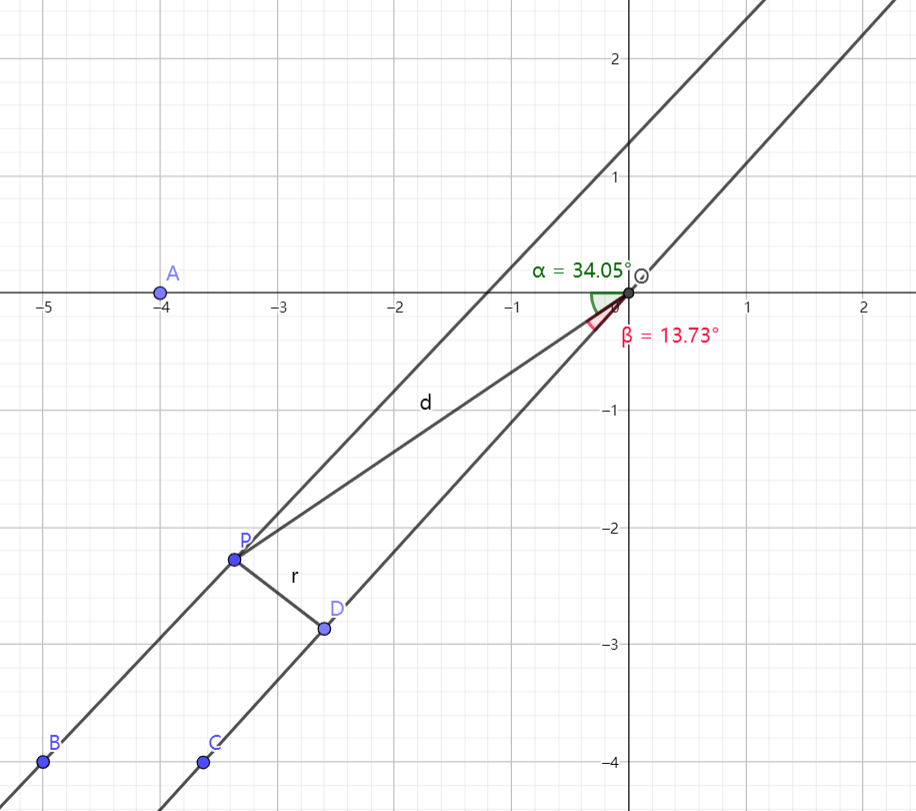
感觉这里需要画图。
以当前枚举的旋转中心为 O，目标点为 P，向量 OP 的长度为 d，笔刷半径为 r。
初始角度 为 -PI 时，笔刷下边界在 x 轴，设当前向量的辐角为 alpha，中间三角形的夹角为 beta。
那么 P 点会被覆盖的区间为 [alpha, alpha+beta] 和 [alpha+PI-beta, alpha+PI]。
如果 d <= r，那么 beta 不存在，只需要考虑 [alpha, alpha+PI]。
然后因为对称性，我们其实只需要扫半个圆，比如 [0, PI] 这个区间，所以在这个题里不拆环也是 ok 的。。。
最后主程序非常短 …
const int N = int(3e3) + 9;
Po P[N];
int n, r;
int main(){
#ifndef ONLINE_JUDGE
//freopen("in.txt", "r", stdin);
//freopen("/Users/minakokojima/Documents/GitHub/ACM-Training/Workspace/out.txt", "w", stdout);
#endif
RD(n, r); REP(i, n) P[i].in();
int z = 2; REP(a, n) {
vector<pair<DB, int>> E;
int s = 1; REP(b, n) if (b != a){
Po v = P[b] - P[a]; DB d = v.len();
DB a = v.arg();
E.PB({a, 1}); E.PB({a + PI, -1});
if (d > r) {
DB b = asin(r/d);
E.PB({a + b, -1});
E.PB({a + PI - b, 1});
}
}
SRT(E); for (auto e: E) checkMax(z, s += e.se);
}
cout << z << endl;
}
Problem J. ‘S No Problem
树形 DP，比 我出的那个题 简单多了。
显然如果只有一条路径的话是个经典题，不妨讨论，如果有 k 条路径的话可以做吗？
我们发现其实是个树上背包。
dp[u][2][5] 表示当前节点的奇偶性，以及子树中一共出现了多少路径的端点，简单转移即可。
Problem B. The Cost of Speed Limits
给定一个边权无向图，对于某个节点，如果其相邻的边里有权值不一样的边，
那么需要在这个点上对每一条出发的边都设置一个限速标牌。
每个限速标牌的代价为 c，增加某条边的单位权值的代价为 1。
问如何修改这张图，使得总代价最少。
另一个树形 dp！
题目其实还不错，但是数据范围非常迷，貌似大家都是 O(n2) 爆过去的。。。
总之这个题争议比较大，参见 maroonrk 的吐槽。
————————
dp[u][i] 表示将这个节点相邻的边全部修改成 i 的代价，
sign[u] 表示所有相邻节点防止限速牌的代价，
best[u] 表示所有 dp[u] 和 sign[u] 的最小值。
那么转移方程有：
sign[u] = c*SZ(adj[u]) + \sum best[v]
dp[u][i] = \sum min(sign[v] + 修改到 v 的边权, dp[v][i]) + 修改到 p 的边权
离散化掉第二维，输出 best[1] 即可，复杂度 O(n2)，注意常数可过。
Problem A. Cardiology
貌似是简单题，但是我读不懂题意。。。。
Problem M. Trailing Digits
给定 b,d,a，求 nb <= a，使得 nb 末尾的数字 d 最多。
不会。。。
Problem H. QC QC
交互式问题，非常经典的测谎问题。
有 n 个人，其中一些人是好人，一些人是坏人，并且每个人都知道所有人分别是好人还是坏人。
你可以询问某个人，另一个人是好人还是坏人，好人总是会告诉你真实信息，坏人可以说谎。
用最少的询问区分好人和坏人。
atcoder 也出过一个版本，
那个题里 n <= 2000，你至多可以询问 2n 次。
这个题里，n <= 100，你至多可以询问 12 轮，每轮次，你需要问所有人一次问题。。。
首先如果坏人 >= 好人那么无解，因为坏人可以绑票伪装成好人然后反咬。
否则肯定有解，因为如果对所有人问一次同一个人，如果有超过半数的人认为它是好人，那么它一定是好人。
接着问这个好人就可以了。不过这样询问次数可能是 n2/2 次。
怎么样在 O(n) 次询问里找到一个好人呢。。。
有一个非常 nice 的方法，
首先这个村子里每个村民都是预言家，
当 A 说 B 是狼人时，只有下面三种情况。
1. 真预言家报查杀。
2. 狼人悍跳诬陷预言家。
3. 狼人出卖自己的狼同伴以做高自己的身份。
不管怎么说，A、B 不会同时为好人。
那么我们只要用栈构造一条询问链，按照顺序用栈顶的元素询问每个人，
如果询问为假，就弹出栈顶，否则就 push 一个新人。
那么 n-1 次询问过后，
假设当前栈中某个人是好人，那么它询问链后面的每个人也都是好人，
所以栈顶的那个人一定场上身份最高的。
有因为在有解的情况下，此时栈中一定至少有一个人是好人，所以栈顶的那个人一定是好人。
这样一共 2(n-1) 次询问就可以知道所有的结果了。
用类似的方法可以解决 WF 的这个题。
