对于有标号图,假设我们得到了不连通情况下的 EGF,那么求对应的连通图有常见套路(可参见 城市规划那个题 和 荒漠那个题)。
因而问题转换为不连通的情况,也就是 上一题。
我们需要先想办法构造卷积。
(1) 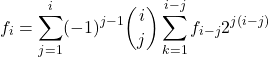
这里需要用一些 trick,最后得到。
(2) 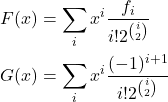
#include <lastweapon/poly>
#include <lastweapon/number>
using namespace lastweapon;
LL C2(LL n) {
return n*(n-1)/2;
}
int main() {
#ifndef ONLINE_JUDGE
//freopen("in.txt", "r", stdin);
#endif
int n; RD(n)++;
Poly F(n); Mint i2 = invFac[2];
FOR(i, 1, n) {
F[i] = invFac[i] * pow(i2, C2(i));
if (i&1) F[i] = -F[i];
}
F[0] += 1; F = F.inv(n);
REP_1(i, n) F[i] *= pow(Mint(2), C2(i));
F = F.log(n);
--n;
REP_1(i, n) {
cout << F[i] * fac[i] << endl;
}
}




 Alca
Alca Amber
Amber Belleve Invis
Belleve Invis Chensiting123
Chensiting123 Edward_mj
Edward_mj Fotile96
Fotile96 Hlworld
Hlworld Kuangbin
Kuangbin Liyaos
Liyaos Lwins
Lwins LYPenny
LYPenny Mato 完整版
Mato 完整版 Mikeni2006
Mikeni2006 Mzry
Mzry Nagatsuki
Nagatsuki Neko13
Neko13 Oneplus
Oneplus Rukata
Rukata Seter
Seter Sevenkplus
Sevenkplus Sevenzero
Sevenzero Shirleycrow
Shirleycrow Vfleaking
Vfleaking wangzhpp
wangzhpp Watashi
Watashi WJMZBMR
WJMZBMR Wywcgs
Wywcgs XadillaX
XadillaX Yangzhe
Yangzhe 三途川玉子
三途川玉子 About.me
About.me Vijos
Vijos
