某岛

… : "…アッカリ～ン . .. . " .. .

January 27, 2013

SPOJ 1479. The GbAaY Kingdom

Problem C. The GbAaY Kingdom

Brief description:

… 最小直径生成树。

Analysis:

容易看出最小直径生成树就是以某个「中心」为根的最短路径树（shortest-paths tree）。。
。这个中心满足，到树上其他点的距离的最大值 —— 「偏心率」（eccentricity）最小。。
..我们称这个点为「绝对中心」（absolute center）。。。。

找出绝对中心后。。我们只要从这个点出发。。遍历出最短路径树就可以求出所有需要的东西。。。
。。于是最小直径生成树问题现在就归约到绝对中心的定位问题。。。
。。比较棘手的是。「绝对中心」。可以出现在某条边的内部。。

。。。假设绝对中心在某条边上 E(x, y, w)。。且距离 x 点的偏移是 o（以下把这个点也记做 o）。。
距离 y 点偏移就是 o’ = w – o。。那么对于任意一个点 i。。其到 o 点的距离就是。。

。。dist(i, a) = min(dist(i, x) + o, o’ + dist(y, i));

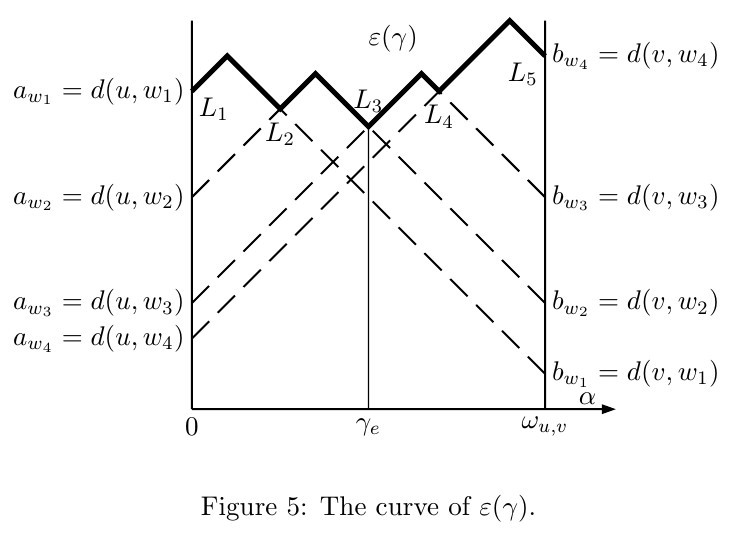
那么关于一个点，把所有偏移位置的距离都绘出就是两条斜率分别为 +1, -1 的折线的取 min。。
。。。关于所有点。。就是一组 +1 -1 的折线。。（取 min 后再取 max。。。

。。折线段由 dist(i, x) 和 dist(i, y) 唯一确定。。。并且。。若某组折线段的 dist(i, x) 和 dist(i, y) 都 ≤ 另一组折线段。。
那么把这组折线段删去对求取「全局最小值」（global minimum）也没有影响。。。称删去所有这种线段的过程为「化简」（simplification）。
。。。注意 simplification 后留下的那玩意似乎不是凸壳（Convex cone）。。。
仅仅只是外边界（upper boundary）。。。

约定：
dm：直径
o：偏心率
de：绝对中心所在边。

        REP(u, n) I[u] = MP(D[a][u], D[b][u]);
        nn = 0; sort(I, I+n); REP(ii, n){
            while (nn && II[nn].se <= I[ii].se) --nn;
            II[++nn] = I[ii];
        }
        if (II[nn].fi < dm){
            dm = II[nn].fi, de = MP(a, b), o = 0;
        }
        if (II[1].se < dm){
            dm = II[1].se, de = MP(a, b), o = w;
        }
        FOR(ii, 1, nn) if ((w + II[ii].fi + II[ii+1].se) / 2 < dm){
            dm = (w + II[ii].fi + II[ii+1].se) / 2, de = MP(a, b);
            o  = (w - II[ii].fi + II[ii+1].se) / 2;
        }

http://vjudge.net/vjudge/problem/viewSource.action?id=2774287（1.82s