250. DivideAndShift

Brief description:

。。求满足以下递归关系的某函数的值。。
f(n, 0) = 1
f(n, m) = f(n, m%n)
f(n, m) = min(f(n, m-1), f(n, m+1), f(n/d, m%(n/d))

Analysis:

。。显然放缩总是安排在滚动的前面比较科学。。。于是枚举约数就行了。。放缩次数等于素因子个数。。

int fact(int x){
    int z = 0; REP(i, SZ(P)){
        while (x % P[i] == 0) ++z, x /= P[i];
        if (x == 1) break;
    }
    if (x != 1) ++z;
    return z;
}

class DivideAndShift {
public:
	int getLeast(int n, int m) {
        sieve(); --m; int res = INF; REP_1(d, n) if (n % d == 0){
            int nn = n / d, mm = m % nn;
            checkMin(res, fact(d) + min(mm, nn-mm));
        }
        return res;
	}
};

500. YetAnotherORProblem
Brief description:
。给定一个长度为 n 的数组 a[]。。求有多少满足条件的数组 b[]。。使得。。b[i] <= a[i]。。。且 b 的和等于位或。。
Analysis:
。。和等于位或。。显然就是每个位上至多有一个一。。于是显然和某题一样。。可以从高位到低位 DP。。。

dp[k][s]: 表示当前第 k 位。。s 表示当前已经不受限制的集合。。。枚举 0 和 恰好有一个 1 这两种决策。记忆化搜索即可。。。
const int N = 10;
int dp[61][1&lt;&lt;N]; vector&lt;long long&gt; R;
int n;

int f(int k, int s){

    if (k &lt; 0) return 1;

    int &amp;res = dp[k][s]; if (res == -1){
        int ss = s; REP(i, n) if (_1(R[i], k)) ss |= _1(i);
        res = f(k-1, ss); // 0 .. .

        REP(i, n) if (_1(s, i) || _1(R[i], k)){ // 1 .. .
            int ss = s; REP(j, n) if (j != i &amp;&amp; _1(R[j], k)) ss |= _1(j);
            INC(res, f(k-1, ss));
        }
    }
    return res;
}

class YetAnotherORProblem {
public:
	int countSequences(vector&lt;long long&gt; R){
	    ::R = R; n = SZ(R); FLC(dp, -1);
		return f(60, 0);
	}
};

1000. BarbarianInvasion2
Brief description:
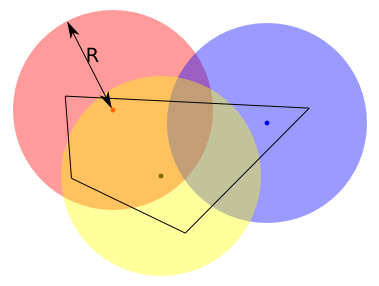
。。一个 n 个点的凸包内部分布着 m 个点。。。要求将凸包的轮廓分割成等长的 m 段测度。。（。注意每段不要求在边界上连续分布。。）。。。将这些测度和内部的点做匹配。。。最小化最远的测度到点的距离。。。(m = 5)
Analysis:
。。首先二分答案。。

。。显然对凸包上的每一条边。。我们需要做线段和圆求交。。然后扫描线。。搞出每个小段可以从属的圆的集合。。。

。。之后要判断合法。。实际上就得到了一个完备匹配的问题。。。似乎可以跑网络流。。但是困难之处在于。。此题中的容量不是整数。。。。

。。注意到。m 非常小。。而且我们只要判断完备匹配的存在性。。所以可以暴力使用 Hall’s marriage theorem。。。
const int M = 5;
VP B; Po C[M]; DB T; DB S[1&lt;&lt;M];
int n, m;

bool f(DB r){

    RST(S); REP(i, n){

        Seg l(B[i], B[i+1]); DB ln = l.len(); vector&lt;DB&gt; D; D.PB(0), D.PB(ln);

        REP(j, m){

            Circle c(C[j], r); if (!~c.sgn(l)) continue;
            Po p0, p1; VP P = c*l; ECH(p, P) D.PB(dist(*p, B[i]));

            /*DB b= 2*dot(B[i]-C[j],l.d()._1()), c = (B[i]-C[j]).len2() - sqr(r);
            DB d = sqr(b) - 4*c; if (d &lt; 0) continue;
            d=sqrt(d); DB d0 = (-b-d)/2, d1 = (-b+d)/2;
            if (0&lt;d0&amp;&amp;d0&lt;ln) D.PB(d0); if (0&lt;d1&amp;&amp;d1&lt;ln) D.PB(d1);*/
        }

        SRT(D); FOR(j, 1, SZ(D)){
            Po p = l.a + l.d()._1()*(D[j]+D[j-1])/2;
            int s = 0; REP(k, m) if (~sgn(r*r, dist2(p, C[k]))) s |= _1(k);
            S[s] += D[j] - D[j-1];
        }
    }

    FOR(s, 1, _1(m)){
        DB p = 0, q = T * count_bits(s);
        FOR(ss, 1, _1(m)) if (s &amp; ss) p += S[ss];
        if (sgn(p, q) &lt; 0) return 0;
    }
    return 1;
}

class BarbarianInvasion2 {
public:
	double minimumTime(vector &lt;int&gt; bX, vector &lt;int&gt; bY, vector &lt;int&gt; cX, vector &lt;int&gt; cY) {

	    n = SZ(bX), m = SZ(cX); B.resize(n+1);
	    REP(i, n) B[i] = Po(bX[i], bY[i]); B[n] = B[0]; T = getPeri(B) / m;
	    REP(i, m) C[i] = Po(cX[i], cY[i]);

		DB l = 0, r = 1e5; DO(233){
		    DB m = (l+r) / 2;
		    if (f(m)) r = m;
		    else l = m;
		}
		return l;
	}
};

External link:
https://apps.topcoder.com/wiki/display/tc/SRM+508

https://gist.github.com/lychees/6475006

www.cnblogs.com/zbwmqlw/archive/2011/06/03/2070534.html
                                                												

													Posted by 
													xiaodao													
													Category: 													TopCoder