DIV 1 Level 1:
Brief description:
给定一个平面图。。每个点的位置坐标不知道。。
问有多少种删边方案。。使得图中不存在交叉边。。
Analysis:
满足条件的图只有两种。。分放射形和三角形讨论。。
const int N = 50;
bool G[N][N];
int deg[N];
class PenguinSledding {
public:
long long countDesigns(int n, vector <int> x, vector <int> y) {
LL res = 1; int m = SZ(x);
RST(deg, G); REP(i, m){
deg[--x[i]]++, deg[--y[i]]++;
G[x[i]][y[i]] = G[y[i]][x[i]] = 1;
}
REP(i, n) res += _1(deg[i]);
REP_3(i, j, k, n, i, j) if (G[i][j] && G[j][k] && G[k][i]) ++res;
res -= n + m;
return res;
}
};
DIV 1 Level 2:
Brief description:
一个企鹅在一个圆环上移动。。位置坐标有 n 个。。开始在 0 点，每一步可以选择顺时针或者逆时针。。第 i 的步长为 i。。
。。问 m 步最终返回 0 的方案有多少种。。（两种方案被称为是不想同的。。如果中间有一步停留的格子不一样。。
Analysis:
略。。（卷积 + 快速幂。。
（代码。。
DIV 1 Level 3:
Brief description:
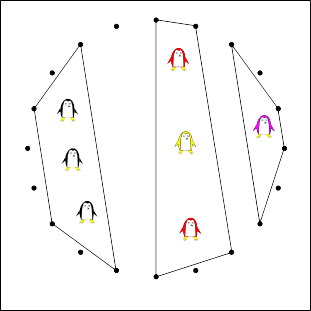
。圆上存在一个 n 个点的内接正多边形。。圆内分布着 m 个企鹅。。每个企鹅有一种颜色。。。
。。选择一些圆环上的点。。围成的多边形称为栅栏。。一组栅栏被称为是合法的。。当且仅当：
- 栅栏之间禁止交叉以及共享某个顶点。
- 栅栏内部至少有一个企鹅。
- 所有企鹅都必须处在一个栅栏内。
- 所有同种颜色的企鹅必须处于同一个栅栏内。
。。计数合法栅栏组的方案数。。
Analysis:
计算几何预处理 + 组合 DP。。
…颜色信息的作用仅在于删边。。如果对角线两侧存在相同颜色的企鹅。。那么任何一种方案中都不可能会有该边出现。。
。。。之后预处理出每条边。。在其逆时针方向上有多少个企鹅。（。这个信息至关重要。。因为需要判断区域为「空」的情况。。
。两个步骤都可以用叉积轻松完成。。（同时在这一步判断无解。。
。。首先。从后往前划分阶段。。。显然要讨论两种状态:。。
- F[s][t]: 当前区间满足题目要求的合法解。
- G[s][t]: 最外层的多边形没有封上。。（凸壳。。
。。。但是转移方程想不清楚。（弱爆了。。）。。于是就去膜拜了一下 Petr 的 Practice Room 里的代码。
。。于是发现少了一种状态。。。
。。之前的 G 不能直接转移到 F。。因为无法确认最外层的多边形，立即被封上后里面是否包含企鹅。。。
因此对 G 增加一个维度。。G[0/1][s][t]。。表示封上后是否合法。。
。（。。F, G0, G1 分别对应 Petr 代码里的 waysFree, waysInside, waysInsidish。。）
。。转移方程是这样。。
.. F <- G1 <- G0 <- F ...
。。呃。。
.. .
RST(F, G); DWN(s, n, 0){
F[s][s] = F[s+1][s] = F[s][s+1] = 1;
G[0][s][s+1] = 1, G[1][s][s+1] = 0;
FOR(t, s+2, n){ // // A[][] 表示对角线逆时针区域内有多少个企鹅。。
if (A[s][t] == A[s+1][t-1] && !del[s][t]){
INC(G[0][s][t], F[s+1][t-1]);
}
FOR(i, s+1, t) if (A[i][t] == A[i+1][t-1] && !del[i][t]){
INC(G[0][s][t], pdt(G[0][s][i], F[i+1][t-1]));
INC(G[1][s][t], pdt(G[A[s][t] == A[s][i] + A[i+1][t]][s][i], F[i+1][t-1]));
}
if (A[s][t] == A[s+1][t]){
INC(F[s][t], F[s+1][t]);
}
FOR_1(i, s+1, t) if (A[s][t] == A[s][i] + A[i+1][t] && !del[s][i]){
INC(F[s][t], pdt(G[1][s][i], F[i+1][t]));
}
}
}
return F[0][n-1];
.. .
